| ■ | General | |||||
|
|
||||||
| ● | When: |
|||||
| Section | Date | Start Time | ||||||||
| 256 | 02-19-2026 (Thursday) | 06:30 pm | ||||||||
| 257 | 02-19-2026 (Thursday) | 05:00 pm | ||||||||
| ● | Duration: 1 hour 20 minutes. | |||||
| ● | Questions can be on anything covered up to the most recent lecture (on 02/17/26). | |||||
| ► | That means the relevant lecture
notes are
001 BigPictures 001 BigPictures_Sup01 - focus on catching the "big piture" (not details of any particular aspects) 001 BigPictures_Sup02 - focus on catching the "big piture" (not details of any particular aspects) 001 BigPictures_Sup03 - focus on catching the "big piture" (not details of any particular aspects) 001a MotivationPushAndRealityCheck 002 DigitalInfoRepresentation01 002_ DigitalDataRepresentationPanoramically 002__ DistinctPatternsWithHybridDigits 003 DigitalInfoRepresentation02 003a SupplementaryLectureNote(forReplacementClass) 004 DigitalInfoRepresentation03 004a SupplementaryLectureNote(forReplacementClassInThePast) 005 DigitalInfoRepresentation04 005 DigitalInfoRepresentation04Sup01(Unicode and UTF-8) 005_ PertinentBinaryEncodingFormulas |
|||||
| ► | More focussed leads: Zoom-Recordings (and associated Key-Resource) postings on class website (Canvas). |
|||||
| ● | Test will be closed books / notes / online-resources / discussion and no calculating devices of any kind are allowed. | |||||
| ► | All allowed reference material (such as IEEE 754 signed real number encoding/decoding schematic and ASCII chart) will be provided as part of the exam. | |||||
| ► | All electronics off during the exam. (In particular: no calculators of any kind allowed.) |
|||||
|
|
||||||
| ■ | Checklist of (most if not all) the things you are expected to know | |||||
|
|
||||||
| ● | Where and how assembly language fits in, relative to: | |||||
| ► | Virtual machine layers (abstraction in hardware). | |||||
| ○ | Instruction Set Architecture (ISA) as interface between hardware and software, in particular. | |||||
| ♯ | Typically specifies instruction set, (general purpose) registers, data types and addressing modes. | |||||
| ♦ |
instruction: primitive operation (task) processor supports (e.g., add) - each has 2 main parts in opcode (operation code) and operands. | ||||||
| ⁃⁃ | First look at CISC (complex instruction set computers) and RISC (reduced instruction set computers). | |||||||
| ♦ |
register: fastest kind of storage device (located on processor chip) of the typical computer. | ||||||
| ⁃⁃ | general-purpose registers: those (assembly-language) programmers get to use to write programs. | |||||||
| ⁃⁃ | 2 special-purpose registers of note: program counter
(PC) and instruction register (IR). (The key roles PC and IR play relative to a first look at the fetch-decode-execute cycle involved in program execution.) |
|||||||
| ♦ |
data type: set of representable values + set of relevant operations (e.g., int). | ||||||
| ♦ |
addressing mode: way of specifying the location(s) of operand(s) involved in an instruction - each operand may be a soure operand or a destination operand. | ||||||
| ♯ | But not implementation. | |||||
| ► | Other programming languages (espcially higher level ones). | |||||
| ○ | 1GL, 2GL, 3GL, 4GL, . . .: machine language is 1GL, assembly language is 2GL and high-level language is 3GL. |
|||||
| ○ | Reflected in typical translation hierarchy for C: compiler --> assembler --> linker --> loader. | |||||
| ♯ | compiler does "high-level language → assembly language" translation. |
|||||
| ♯ | assembler does "assembly language → machine language" translation. |
|||||
| ● | In terms of lines of code needed to express a computation, how is assembly language typically different compared to high-level languages. | |||||
| ► | To accomplish the same thing, assembly language typically requies more lines of code than high-level language. | |||||
| ● | Advantages/disadvantages, common application areas and truths and half-truths of assembly language. | |||||
| ► | Undeniable truth: not portable (e.g.: assembly language program written to run on MIPS will not run on INTEL). | |||||
| ● | Meaning of digital and digital system. | |||||
| ● | Characteristics/implications/consequences/. . . of/for being digital. | |||||
| ► | Discrete and finite (as opposed to continuous and infinite that apply to analog). | |||||
| ► | sn # of (distinct/unique) states associated with digital system (s = # of digital variations, n = # of digits involved). | |||||
| ► | s1 х s2 х . . . х sn # of (distinct/unique) states associated with hybrid digital system (s1 = # of digital variations of digit 1, . . ., sn = # of digital variations of digit n). | |||||
| ► | Partial (selective/discrete) represention to deal with digital-reality mismatch often encountered. | |||||
| ● | Present-day's predominate finite-state device. | |||||
| ► | Transistor - electronic - switching (not regulating) circuit - 2-state (not 3-or-more-state) - binary - why. | |||||
| ● | How many unique values (or range of zero-and-higher whole numbers) a given set of finite-state devices (i.e., bits or "tit"s or "qit"s etc.) is able to represent. | |||||
| ● | Minimum number of bits (or "tit"s or "qit"s etc.) required to represent a given number of unique values (or range of zero-and-higher whole numbers). | |||||
| ● | How bits (or "tit"s or "qit"s etc.) can be used to represent anything. | |||||
| ► | Can encode/represent anything with numbers. | |||||
| ○ | (Each of us is treated/represented as numbers often enough!) | |||||
| ► | Can represent any finite number of numbers if finite-state devices are available in sufficient number. | |||||
| ● | What 2 basic strategies for binary encoding of set of items (such as set of values) are. | |||||
| ► | Base it on mathematical formula. | |||||
| ► | Base it on assigned item-pattern mapping - typically crafted in some way (and not arbitrarily). | |||||
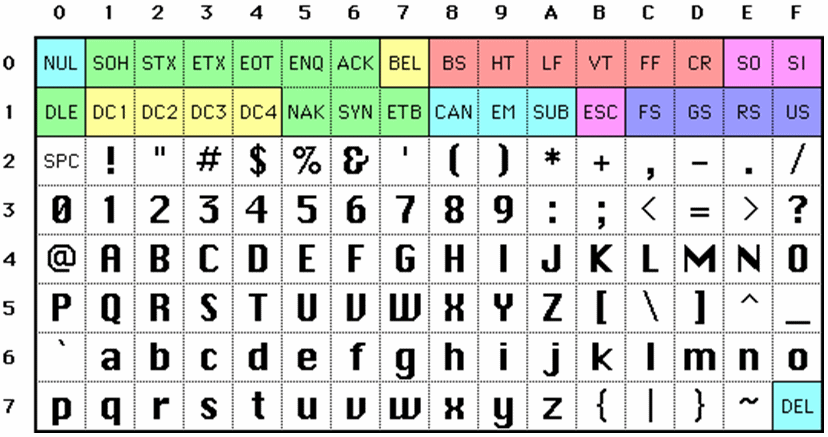
| ● | Know about ASCII code and Unicode. | |||||
| ► | In particular: how is Unicode different than ASCII code, and why (-> globalization / internationalization). | |||||
| ► | For backward compatibility, the first 128 Unicode characters point to ASCII characters. | |||||
| ○ | (some allude to this by saying that ASCII is a subset of Unicode) | |||||
| ● | ASCII character encoding in more detail. | |||||
| ► | Some key characteristics: | |||||
| ○ | The positive whole number the byte (encoding a character) evaluates to is the ASCII value of the character. | |||||
| ○ | Characters representing digits come before (have lower ASCII values) than letters (alphabets) and appear consecutively in increasing order of ASCII value. | |||||
| ○ | The ASCII value of the character representing 0 ('0') is not 0. | |||||
| ♯ | The character with ASCII value 0 is the null character ('\0') that is used as the null terminator in C-strings. | |||||
| ○ | Uppercase letters (alphabets) come before (have lower ASCII values) than lowercase letters (alphabets) and appear consecutively in increasing order of ASCII value. | |||||
| ○ | Lowercase letters (alphabets) come after (have higher ASCII values) than uppercase letters (alphabets) and appear consecutively in increasing order of ASCII value. | |||||
| ○ | An uppercase letter (alphabet) and it's lowercase counterpart appear in the same column on the ASCII chart. | |||||
| ♯ | Their bit patterns differ by only 1 bit (the 5th bit, with the least significant bit being the 0th bit). | |||||
| ♯ | 'a' does not come immediately after 'Z' (but there's a 6-character gap between them) on the ASCII chart. | |||||
| ► | In particular: understand and know
how to apply the following (in part or in whole). |
|||||
 |
||||||
| ● | How positional numbers are defined for unsigned whole numbers and fractions and how to use the definition in evaluations. | |||||
| ► | (Our scope confined to the usual way the numbers are represented that we looked at, i.e., representations based on radix polynomials.) | |||||
| ● | What Horner's scheme is and where and how it can be used to effect efficient evaluations. | |||||
| ► | The double-and-add method for evaluating unsigned binary numbers. | |||||
| ► | Extended use in other mathematically similar settings: triple-and-add, quadruple-and-add, . . . for ternary (base-3), quarternary (base-4), . . . numbers. | |||||
| ● | How to convert decimal whole numbers to binary using the repeated subtraction and repeated division methods. | |||||
| ► | Similarly for converting decimal whole numbers to ternary, quarternary, . . . | |||||
| ● | How to convert decimal fractions to binary using the repeated multiplication method. | |||||
| ● | How to quickly translate a hex digit into the equivalent 4 binary digits and vice versa. | |||||
| ● | How to convert from binary (both whole numbers and unsigned real numbers) to hex and hex to binary. | |||||
| ● | Know the rules for and use them to perform binary addition. | |||||
| ● | The 4 different methods (as discussed in class) for representing signed whole numbers, their characteristics, and some key reasons for the predominant use of 2's complement. | |||||
| ► | SM, 1C, 2C, Bias (Excess) | |||||
| ● | The polynomial representation for a 2's complement number and the associated Horner's scheme for evaluating the decimal equivalent of a 2's complement number. | |||||
| ● | How to quickly find the 2's complement of a binary number, i.e., without having to first find the 1's complement and then add 1. | |||||
| ● | What overflow is. | |||||
| ► | Know the key advantage 2C has (over SM and 1C) --> main reason most modern computers use 2C to represent signed whole numbers. |
|||||
| ○ | Same way (thus device) used to "add unsigned whole numbers" and "add signed whole numbers" --> just have to detect overflow differently. | |||||
| ● | How to detect overflow when performing addition involving unsigned numbers and when involving 2's complement numbers | |||||
| ► | By examining the state(s) of certain bit(s) in 1 or 2 positions. | |||||
| ► | List of observations (note that each is in terms of the state(s) of certain bit(s) in 1 or 2 positions -- something that can be easily made in hardware): | |||||
| - carry-out is 0 when bits at most-significant-bit position are added. - carry-out is 1 when bits at most-significant-bit position are added. - addends have opposite signs. - addends are both positive, sum is positive. - addends are both positive, sum is negative. - addends are both negative, sum is positive. - addends are both negative, sum is negative. - carry-in and carry-out at most-significant-bit position are the same. - carry-in and carry-out at most-significant-bit position are not the same. |
||||||
| ● | How to quickly arrive at the range of 2's complement numbers a given number of bit can represent (in terms of powers of 2). | |||||
| ► | Range for n-bits: [ -2n-1 , 2n-1 - 1 ] | |||||
| ● | How to derive ballpark ideas about 2's complement numbers (comparative ideas about them: negative or positive and relatively more negative or positive). | |||||
| ● | Know about lengthening/shortening of binary whole numbers (unsigned or 2's complement) and when the operations are needed/appropriate. | |||||
| ► | In particular: zero-extension and sign-extension. | |||||
| ► | (Note that "more compact (shorthand) representation in hex" of the binary whole numbers involved may be called for.) | |||||
| ● | How oddness/evenness (in general, divisibility by some power of 2) can be quickly determined for signed/unsigned whole numbers represented in binary and hex. | |||||
| ● | Know the key features of IEEE 754-1985 single-precision and double-precision formats. | |||||
| ► | Sign bit, biased exponent, fraction (or significand or mantissa) and hidden bit. | |||||
| ● | How to encode and decode a signed floating-point number in IEEE 754-1985 single-precision and double-precision formats. | |||||
| ► | Understand and know how to apply the following (in part or in whole): | |||||
 |
||||||
| ● | How to derive ballpark ideas about signed floating-point number in IEEE 754-1985 (comparative ideas about them: negative or positive and relatively more negative or positive). | |||||
|
|
||||||
| ■ | Other | |||||
|
|
||||||
| ● | Use Assignment 1 (all 3 parts) as part of your preparation. | |||||
| ► | ||||||
|
| (In particular: Expect significant number of conceptual questions, noting that pretty much all assignments have been quantitative.) |
|||||
| ● | Take advantage of relevant drills and challenges exercises posted on the class homepage (under Drills And Challenges). | |||||
| ► | ||||||
| ● | You may want to check out sample past exam questions posted on the class homepage (under Other Resources). | |||||
| ► | You should not however, expect the questions to be identical in number, kind, topic coverage, etc. | |||||
| ► | Notion very ill-advised to harbor: I take it I will do well in current exams if I can do the sample past exam questions well. |
|||||
| ► | You should not have to worry about questions being written on topics we have not (or not yet) covered; some such questions may appear as sample past questions because the associated topics were appropriate at that time. | |||||
| ● | Do the following if you are eligible and intend to use extended time accommodation: | |||||
| ► | Follow proper procedure to request taking the exam at the ATSD. | |||||
| ○ | You typically need to do the request at least a certain number of (non-weekend?) hours in advance. | |||||
| ○ | The exam date of your request should be the same as the (regularly) scheduled date of the exam. | |||||
| ○ | The exam start time of your request should be closest to the (regularly) scheduled start time of the exam. | |||||