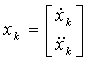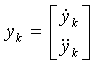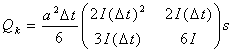Kalman Filtering

A Kalman filter works with a dynamic system that is modeled by an n-by-1 state vector that is updated through a discrete time equation:

In the equation above, A is an n-by-n state transition matrix, B is an n-by-m optional control input matrix, which relates control vector m-by-1 u_k to the dynamic system’s state x_k. w is an n-by-1 process noise vector with covariance Q_k.

We should note that here lower-case, bold letters denote vectors, and upper-case, bold letters denote matrices.

Every dynamic system’s state has a j-by-1 observation/measurement vector:

H is a j-by-n observation model matrix that maps the true state into the observed space. v_k is an observation noise j-by-1 vector with covariance R_k.

The Discrete Kalman filter has two distinct phases that compute the next dynamic system state’s estimate.

Predict:

project the state vector ahead:

project the error covariance matrix ahead:

The predict phase uses the state estimate information from the past time step to produce an estimate for the future state.

Update:

compute the Kalman gain:

update the estimate of the state vector with a measurement z_k:

update the error covariance matrix:

Once the future step becomes current, the new measurement information is used to refine the prediction made in the predict phase, which allows the Kalman Filter to derive a more precise dynamic systems state’s estimate.

Attention Focus Kalman Filter Design

We model an eye as a system that has two state vectors x_k and y_k.

where represents the horizontal and presents vertical eye position on the screen. ,  present the horizontal and vertical eye-velocity, respectively, at the time k.

The state transition matrix for both horizontal and vertical states is:

where is the system’s eye-gaze sampling interval.

The observation model matrix for both state vectors is:

The standard deviation for the instrument noise relates to the accuracy of the eye-tracker equipment and is bounded by one degree of the visual angle, thus making the standard deviation of measurement noise ∂_v=1.

In our AFKF model we use the process noise covariance matrix which was developed by Kohler. This matrix was specifically designed for a process with the translational motion of constant velocity and random acceleration.