Prefix, Infix and Postfix Notations
We are familiar with writing an expression like
When we do so, we are actually using the infix notation. This is not the only notation that can be used. In using the infix notation, we write the operator that is to operate on the operands in between the operands. In the example above, the expression contains two sub-expressions, namely(2 + 3) * 7
andoperand operator operand
2 + 3
Intuitively, instead of writing expressions so that an operator appears in between the operands it is to operate on, we can also write them so that the operator appears before or after the operands. These two alternative ways correspond to the prefix notation and postfix notation, respectively.operand operator operand
(2+3) * 7
For the above example, using the prefix notation results in
andoperator operand operand
+ 2 3
On the other hand, using the postfix notation results inoperator operand operand
* + 2 3 7
andoperand operand operator
2 3 +
Notice that I have conveniently dropped the parentheses for the expressions written in the prefix and postfix notations. This is because they are not needed, which is an advantage that the two alternative notations have over the usual infix notation. Another advantage that is enjoyed by the postfix notation is that expressions written using the notation are particularly easy to evaluate. Some computers internally use postfix notation because of this ease of expression evaluation. Before we examine how easy it is to evaluate a postfix expression, here is a more complex example of an expression written in the three notations:operand operand operator
2 3 + 7 *
Using Stacks to Evaluate Postfix Expressions( 7 + ( 3 * 5 ) ) - 4 (infix)
7 3 5 * + 4 - (postfix)
- + 7 * 3 5 4 (prefix)
The assumptions:
It uses only one stack (for storing numbers --> numbers stack).The algorithm:
There's no need for an operators stack because each operator is used as soon as it is read.
Scan input from left to rightE.g.: Use a stack to evaluate 5 3 2 * + 4 - 5 +
if (input is a number)
push it onto the stack
else if (input is an operator)
obtain 2 numbers from, and pop them off, the stack
peform the operation (NOTE: 2nd number obtained must
be made the left operand)
push the result onto the stack
else
do nothing (simply discard input)
The stack now contains the desired result
(NOTE: In the following, the stack has the top to the right.)(Click here to print the above algorithm and example on one page for quick reference.)Symbol Stack Remarks
------ ----- -------
5 5
3 5 3
2 5 3 2
* 5 6 3 * 2 = 6
+ 11 5 + 6 = 11
4 11 4
- 7 11 - 4 = 7
5 7 5
+ 12 7 + 5 = 12
Answer: 12
Using Stacks to Translate from Infix to Postfix (Fully Parenthesized Case)
The assumptions:
Move each operator to the location of the ')' corresponding to the operation and then remove all parentheses.Some technical details:

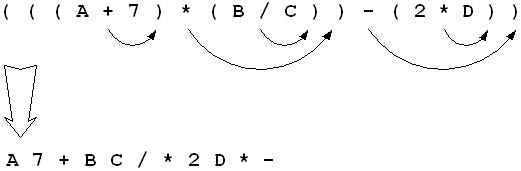
Scan infix expression from left to rightE.g.: Use a stack to translate ( ( ( A + 7 ) * ( B / C ) ) - ( 2 * D ) ) to postfix
if (input is a left parenthesis)
push it onto the stack
else if (input is an operand)
write it to output
else if (input is an operator)
push it onto the stack
else // input is a right parenthesis (spaces are simply discarded)
discard input
if (top of the stack contains an operator)
read from the stack and write the operator read to output
pop the operator off the stack
else // too few operators in the infix expression
print error message and exit
if (top of the stack contains a left parenthesis)
pop the stack
else // infix expression doesn't have balanced parentheses
print error message and exit
Check error status
if (the stack is empty)
all done
else // infix expression is not fully parenthesized
print error message and exit
(NOTE: In the following, the stack has the top to the right.)(Click here to print the above algorithm and example on one page for quick reference.)Symbol Stack Output
------ ----- ------
( (
( ( (
( ( ( (
A ( ( ( A
+ ( ( ( + A
7 ( ( ( + A 7
) ( ( A 7 +
* ( ( * A 7 +
( ( ( * ( A 7 +
B ( ( * ( A 7 + B
/ ( ( * ( / A 7 + B
C ( ( * ( / A 7 + B C
) ( ( * A 7 + B C /
) ( A 7 + B C / *
- ( - A 7 + B C / *
( ( - ( A 7 + B C / *
2 ( - ( A 7 + B C / * 2
* ( - ( * A 7 + B C / * 2
D ( - ( * A 7 + B C / * 2 D
) ( - A 7 + B C / * 2 D *
) A 7 + B C / * 2 D * -
(Stack is empty: all done)
Using Stacks to Translate from Infix to Postfix (General Case)
The assumptions:
Infix expression is fully parenthesizedKey to overcoming "missing" parentheses:
Use precedence rules to help determine the order of operations that are "missing" parentheses.C++ rules for evaluating arithmetic expressions that are not fully parenthesized:
E.g.: Use a stack to translate 3 * X + ( Y - 12 ) - Z to postfixScan infix expression from left to right
if (input is a left parenthesis)
push it onto the stack
else if (input is an operand)
write it to output
else if (input is an operator)
do until (stack is empty OR
top of stack is a left parenthesis OR
top of stack is an operator w/ lower precedence than input)
read the stack and write the result to output
pop the stack
push input onto the stack
else // input is a right parenthesis (spaces are simply discarded)
discard input
do until (stack is empty OR
top of stack is a left parenthesis)
read the stack and write the result to output
pop the stack
if (stack is empty) // unbalanced parentheses
print error message and exit
else // top of stack is a left parenthesis
pop the stack
Finish up and check error status
do until (stack is empty)
if (top of stack is a left parenthesis) // unbalanced parentheses
print error message and exit
else
read the stack and write the result to output
pop the stack
(NOTE: In the following, the stack has the top to the right.)(Click here to print the above algorithm and example on one page for quick reference.)Symbol Stack Output
------ ----- ------
3 3
* * 3
X * 3 X
+ + 3 X *
( + ( 3 X *
Y + ( 3 X * Y
- + ( - 3 X * Y
12 + ( - 3 X * Y 12
) + 3 X * Y 12 -
- - 3 X * Y 12 - +
Z - 3 X * Y 12 - + Z
3 X * Y 12 - + Z -
(Stack is empty: all done)
Textbook Reading
Section 7.4.